Introduction to the computational algorithm

The main difficulty in radiative transfer calculations is the coupling between all the points in the emitting volume. This coupling is caused by dust scattering and thermal emission, which turns every point in space into an energy source. Additionally, the dust thermal emission is controlled by its temperature, which is determined by the unknown radiation field. In a multidimensional dust density configuration there is often an additional problem associated with the dust creation/destruction when it reaches the sublimation temperature.

In LELUYA, the scattering-induced coupling between N grid points is described through an NxN correlation matrix. N can be the total number of points or a subset of grid points. This approach proved to be very efficient in DUSTY. The intensity at these grid points is deduced directly from the inverted correlation matrix and the thermal energy. The main computational effort is to calculate the matrix elements and, therefore, smaller N is computationally preferable. A small number of grid points is also advantageous from the memory point of view to avoid large correlation matrices.

Figure 1: The main computational loop in LELUYA.

The computational effort is huge for the type of problems we would like to solve because they cannot be described with a small N. Thus, a parallelization was implemented into LELUYA right from the start. Overall, we had to invent several new algorithms to make this numerical approach possible since nothing similar to our unstructured grid has ever been tried before in radiative transfer codes. The new algorithms include a spatial grid generator (which is the key element for the success of our method), an angular grid generator, a radiative transfer method, a parallelization technique, and even post-processing techniques for the final output.

LELUYA’s input requires the spectral shape of the central energy source; the chemical and physical properties of each dust component, including its absorption and scattering coefficients and sublimation temperature; the (axisymmetric) dust density distribution; and the total optical depth at one wavelength along one radial ray through the dust cloud. The output lists the spectral energy distribution at arbitrary viewing angles together with the 2D images at all wavelengths, the dust temperature distribution and the bolometric flux at various points (also used for calculating the luminosity).

          
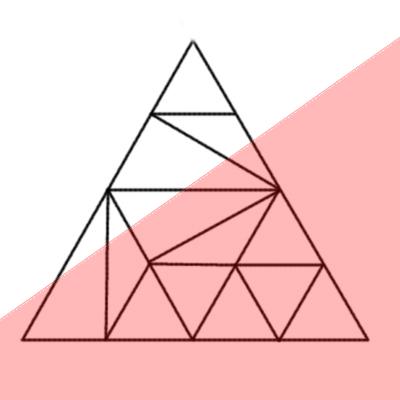
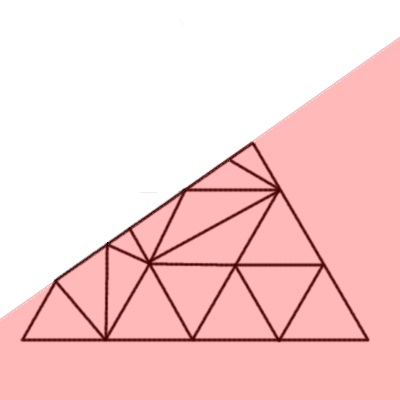
Figure 2: A sequence of steps in the grid generation.

The grid has to contain the optimal number of points for the gradients of both the dust density and optical depth distributions, and each of these poses very different requirements; a grid based on one of the two may be totally inadequate for the other. The relationship between the two is a complicated non-linear function of the spatial and optical depth distances to the edge. This function is crucial for achieving desired numerical precision with a relatively small number of points. LELUYA generates recursively a triangular grid, refining its resolution in each step as shown in figure 2.

To calculate how much energy is streaming from all directions into one point in space, we have to integrate through the whole 3D computational volume. This can be a cumbersome job if the number of rays is not optimized. The angular distribution of these rays has to predict directions where most of the energy is coming from and resolve these sources.

Figure 3: An angular grid on a unit halfsphere. The area of each spherical triangle is used as a weight factor for the integrals along lines through the centers of the triangles.

The search starts with an icosahedron and continues with a recursive division of the spherical triangles on a unit half-sphere (the full sphere is not needed because of the axial symmetry). The area of these triangles is used as a weight factor DW in the sum that represents the angular integral over 4p steradian:

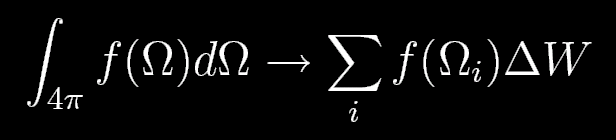
The integration rays pass through the centers of the triangles. An example of the angular grid is shown in figure 3. Parallelization is not common in exact radiative transfer codes. The main reason is that most are 1D codes that perform well on a single processor, while the few multidimensional codes have not yet reached that development stage. LELUYA is a first, employing a parallel method with different processors calculating different rows of the correlation matrix. After these matrices are calculated, another parallelization is included in the LU-decomposition during the matrix inversion. Finally, calculation of the luminosity conservation is parallelized separately.